Ferromagnetic kagome lattice
We create the kagome lattice with up to 4th neighbor interactions. The symmetry related atoms are denoted by MCu1(i)_j, where i is the index of independent atomic positions, j is the index of the generated atomic positions of the i-th independent position.
Contents
Define the lattice
kagome4 = spinw; kagome4.genlattice('lat_const',[6 6 8],'angled',[90 90 120],'spgr','P -3'); kagome4.addatom('r', [1/2 0 0],'S', 1,'label','MCu1','color','r'); disp('Atomic positions:') kagome4.table('atom') plot(kagome4) swplot.zoom(1.5)
Atomic positions:
ans =
3×4 table
matom idx S pos
______ ___ _ _________________
'MCu1' 1 1 0.5 0 0
'MCu1' 2 1 0 0.5 0
'MCu1' 3 1 0.5 0.5 0
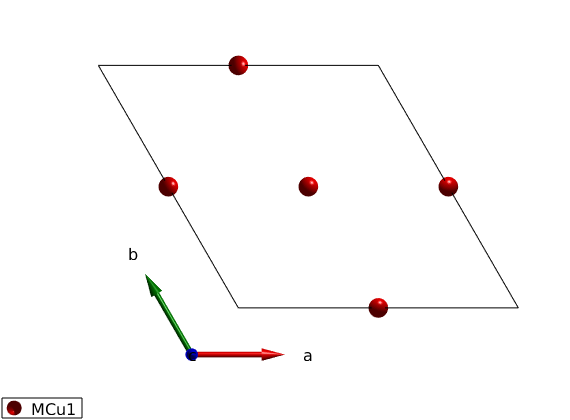
Define Hamiltonian
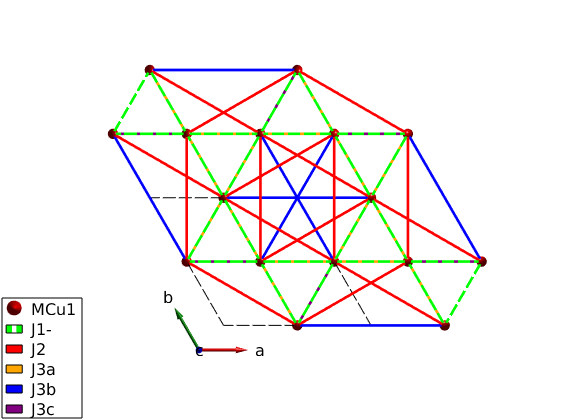
We add couplings up to 4th neighbor interactions. If the generation of the bond tables would depend on distance, J3a, J3b and J3c would be equivalent. However using the 'P -3' space group the three type of bonds are inequivalent, as physically expected in real systems (J3a goes through an intermediate magnetic atom, while the other two bonds are not).
kagome4.gencoupling('maxDistance',7); disp('Bonds:') kagome4.table('bond',[]) kagome4.addmatrix('label','J1-','value',-1.00,'color','g') kagome4.addmatrix('label','J2','value', 0.10,'color','r') kagome4.addmatrix('label','J3a','value', 0.00,'color','orange') kagome4.addmatrix('label','J3b','value', 0.17,'color','b') kagome4.addmatrix('label','J3c','value', 0.00,'color','purple') kagome4.addcoupling('mat','J1-','bond',1); kagome4.addcoupling('mat','J2','bond',2); kagome4.addcoupling('mat','J3a','bond',3); kagome4.addcoupling('mat','J3b','bond',4); kagome4.addcoupling('mat','J3c','bond',5); % The first neighbor bonds will be shown as dashed lines. This is automatic % when the matrix labels ends with a minus sign. plot(kagome4,'range',[2 2 1],'bondMode','line','bondLineWidth0',2)
Bonds:
ans =
21×10 table
idx subidx dl dr length matom1 idx1 matom2 idx2 matrix
___ ______ ______________ ____________________ ______ ______ ____ ______ ____ ______________
1 1 0 1 0 0 0.5 0 3 'MCu1' 3 'MCu1' 1 '' '' ''
1 2 0 -1 0 -0.5 -0.5 0 3 'MCu1' 1 'MCu1' 2 '' '' ''
1 3 0 0 0 0.5 0 0 3 'MCu1' 2 'MCu1' 3 '' '' ''
1 4 0 0 0 0 -0.5 0 3 'MCu1' 3 'MCu1' 1 '' '' ''
1 5 1 0 0 0.5 0.5 0 3 'MCu1' 1 'MCu1' 2 '' '' ''
1 6 -1 0 0 -0.5 0 0 3 'MCu1' 2 'MCu1' 3 '' '' ''
2 1 1 -1 0 0.5 -0.5 0 5.196 'MCu1' 1 'MCu1' 2 '' '' ''
2 2 0 1 0 0.5 1 0 5.196 'MCu1' 2 'MCu1' 3 '' '' ''
2 3 -1 0 0 -1 -0.5 0 5.196 'MCu1' 3 'MCu1' 1 '' '' ''
2 4 0 0 0 -0.5 0.5 0 5.196 'MCu1' 1 'MCu1' 2 '' '' ''
2 5 -1 -1 0 -0.5 -1 0 5.196 'MCu1' 2 'MCu1' 3 '' '' ''
2 6 1 1 0 1 0.5 0 5.196 'MCu1' 3 'MCu1' 1 '' '' ''
3 1 0 1 0 0 1 0 6 'MCu1' 1 'MCu1' 1 '' '' ''
3 2 -1 -1 0 -1 -1 0 6 'MCu1' 2 'MCu1' 2 '' '' ''
3 3 1 0 0 1 0 0 6 'MCu1' 3 'MCu1' 3 '' '' ''
4 1 0 1 0 0 1 0 6 'MCu1' 2 'MCu1' 2 '' '' ''
4 2 -1 -1 0 -1 -1 0 6 'MCu1' 3 'MCu1' 3 '' '' ''
4 3 1 0 0 1 0 0 6 'MCu1' 1 'MCu1' 1 '' '' ''
5 1 0 1 0 0 1 0 6 'MCu1' 3 'MCu1' 3 '' '' ''
5 2 -1 -1 0 -1 -1 0 6 'MCu1' 1 'MCu1' 1 '' '' ''
5 3 1 0 0 1 0 0 6 'MCu1' 2 'MCu1' 2 '' '' ''
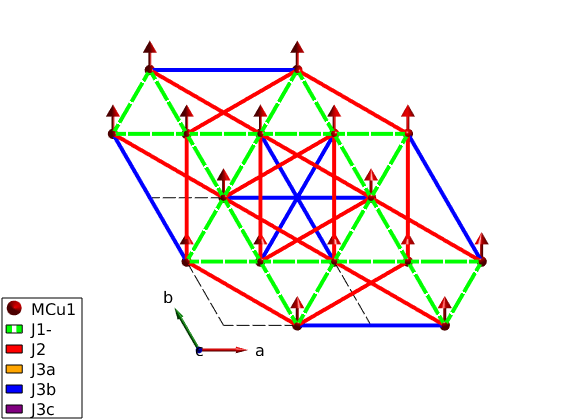
Magnetic structure
For strong FM 1str neighbour and weak further neighbor interaction the ground state is ferromagnetic.
kagome4.genmagstr('mode','helical','k',[0 0 0],'n',[0 1 0],'S',[0 1 0]'); disp('Magnetic structure:') kagome4.table('mag') kagome4.energy plot(kagome4,'range',[2 2 1],'bondMode','line','bondLineWidth0',3,... 'bondZero',false)
Magnetic structure:
ans =
3×7 table
num matom idx S realFhat pos kvect
___ ______ ___ _ ___________ _________________ ___________
1 'MCu1' 1 1 0 1 0 0.5 0 0 0 0 0
2 'MCu1' 2 1 0 1 0 0 0.5 0 0 0 0
3 'MCu1' 3 1 0 1 0 0.5 0.5 0 0 0 0
Ground state energy: -1.630 meV/spin.
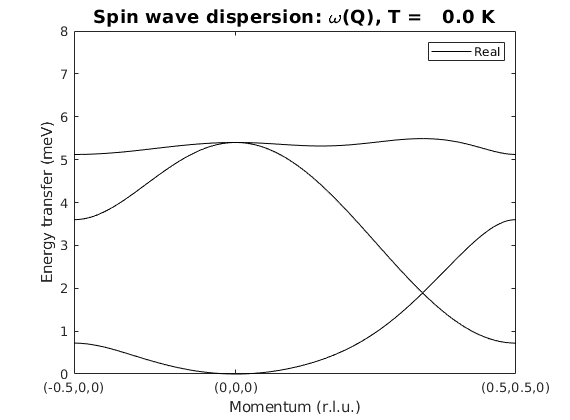
Spin wave dispersion
kag4Spec = kagome4.spinwave({[-1/2 0 0] [0 0 0] [1/2 1/2 0] 200});
kag4Spec = sw_neutron(kag4Spec);
kag4Spec = sw_egrid(kag4Spec,'Evect',linspace(0,6.5,100)) ;
figure
sw_plotspec(kag4Spec,'mode',1,'axLim',[0 8],'colorbar',false,'colormap',[0 0 0])
Warning: To make the Hamiltonian positive definite, a small omega_tol value was added to its diagonal!
Powder averaged spectrum
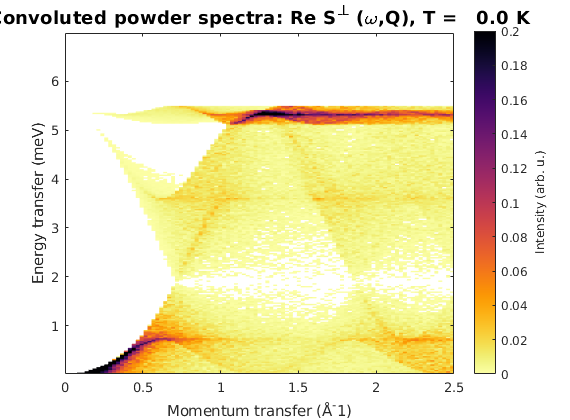
kag4Pow = kagome4.powspec(linspace(0,2.5,100),'Evect',linspace(0,7,250),... 'nRand',1e3,'hermit',false); figure sw_plotspec(kag4Pow,'axLim',[0 0.2],'colorbar',true)
Written by Bjorn Fak & Sandor Toth 06-Jun-2014, 06-Feb-2017