sqrt(3) x sqrt(3) Kagome antiferromagnet
We create a lattice with space group "P -3" where all first neighbor bonds are symmetry equivalent and add a magnetic Cr+ with S=1 spin.
Contents
Define the lattice
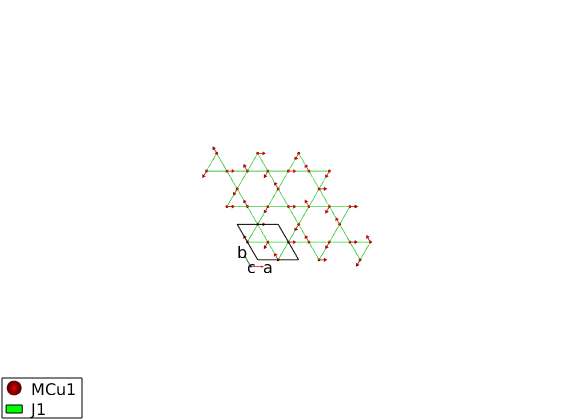
AF33kagome = spinw; AF33kagome.genlattice('lat_const',[6 6 40],'angled',[90 90 120],'spgr','P -3') AF33kagome.addatom('r',[1/2 0 0],'S', 1,'label','MCu1','color','r') plot(AF33kagome,'range',[2 2 1/2],'cellMode','inside')
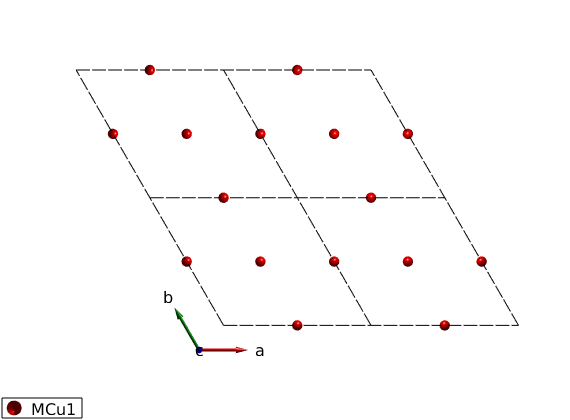
Create bonds
Generate the list of bonds and list the first and second neighbor bonds.
AF33kagome.gencoupling('maxDistance',7) disp('First neighbor bonds:') AF33kagome.table('bond',1)
First neighbor bonds:
ans =
6×10 table
idx subidx dl dr length matom1 idx1 matom2 idx2 matrix
___ ______ ______________ ____________________ ______ ______ ____ ______ ____ ______________
1 1 0 1 0 0 0.5 0 3 'MCu1' 3 'MCu1' 1 '' '' ''
1 2 0 -1 0 -0.5 -0.5 0 3 'MCu1' 1 'MCu1' 2 '' '' ''
1 3 0 0 0 0.5 0 0 3 'MCu1' 2 'MCu1' 3 '' '' ''
1 4 0 0 0 0 -0.5 0 3 'MCu1' 3 'MCu1' 1 '' '' ''
1 5 1 0 0 0.5 0.5 0 3 'MCu1' 1 'MCu1' 2 '' '' ''
1 6 -1 0 0 -0.5 0 0 3 'MCu1' 2 'MCu1' 3 '' '' ''
Hamiltonian
We create AFM first neighbor interactions.
AF33kagome.addmatrix('label','J1','value',1.00,'color','g') AF33kagome.addcoupling('mat','J1','bond',1) plot(AF33kagome,'range',[2 2 1/2],'cellMode','inside')
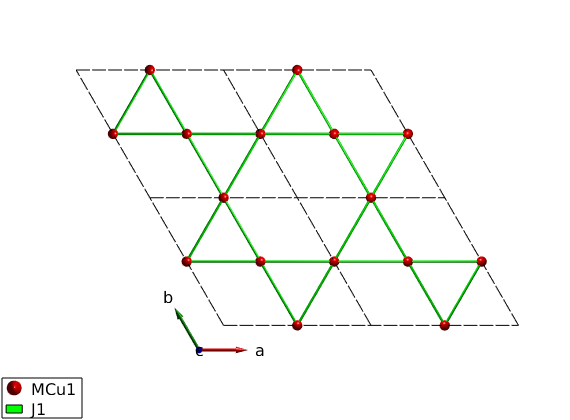
Generate magnetic structure I.
We create the k = (1/3 1/3 0) magnetic structure, with the three spin directions in the unit cell (120 degree between neighbors). The spin vector components are given in the coordinate system of the lattice vectors (abc). We have two possibilities to store the structure. Either we use the magnetic supercell 3x3x1 times the unit cell and in this case the spin waves are calculated on the larger cell that is a zero-k structure.
S0 = [0 0 -1; 1 1 -1; 0 0 0]; AF33kagome.genmagstr('mode','helical','k',[-1/3 -1/3 0],... 'n',[0 0 1],'unit','lu','S',S0,'nExt',[3 3 1]); disp('Magnetic structure:') AF33kagome.table('mag') AF33kagome.energy plot(AF33kagome,'range',[3 3 1/2],'cellMode','inside')
Magnetic structure:
ans =
27×8 table
num matom idx S realFhat imagFhat pos kvect
___ ______ ___ _ ________________________ __________________________ _________________ ________________________________
1 'MCu1' 1 1 -0.5 0.866 0 -0.866 -0.5 0 0.5 0 0 -0.33333 -0.33333 0
2 'MCu1' 2 1 -0.5 0.866 0 -0.866 -0.5 0 0 0.5 0 -0.33333 -0.33333 0
3 'MCu1' 3 1 -0.5 -0.866 0 0.866 -0.5 0 0.5 0.5 0 -0.33333 -0.33333 0
4 'MCu1' 1 1 1 0 0 0 1 0 1.5 0 0 -0.33333 -0.33333 0
5 'MCu1' 2 1 1 0 0 0 1 0 1 0.5 0 -0.33333 -0.33333 0
6 'MCu1' 3 1 -0.5 0.866 0 -0.866 -0.5 0 1.5 0.5 0 -0.33333 -0.33333 0
7 'MCu1' 1 1 -0.5 -0.866 0 0.866 -0.5 0 2.5 0 0 -0.33333 -0.33333 0
8 'MCu1' 2 1 -0.5 -0.866 0 0.866 -0.5 0 2 0.5 0 -0.33333 -0.33333 0
9 'MCu1' 3 1 1 0 0 0 1 0 2.5 0.5 0 -0.33333 -0.33333 0
10 'MCu1' 1 1 1 0 0 0 1 0 0.5 1 0 -0.33333 -0.33333 0
11 'MCu1' 2 1 1 0 0 0 1 0 0 1.5 0 -0.33333 -0.33333 0
12 'MCu1' 3 1 -0.5 0.866 0 -0.866 -0.5 0 0.5 1.5 0 -0.33333 -0.33333 0
13 'MCu1' 1 1 -0.5 -0.866 0 0.866 -0.5 0 1.5 1 0 -0.33333 -0.33333 0
14 'MCu1' 2 1 -0.5 -0.866 0 0.866 -0.5 0 1 1.5 0 -0.33333 -0.33333 0
15 'MCu1' 3 1 1 0 0 0 1 0 1.5 1.5 0 -0.33333 -0.33333 0
16 'MCu1' 1 1 -0.5 0.866 0 -0.866 -0.5 0 2.5 1 0 -0.33333 -0.33333 0
17 'MCu1' 2 1 -0.5 0.866 0 -0.866 -0.5 0 2 1.5 0 -0.33333 -0.33333 0
18 'MCu1' 3 1 -0.5 -0.866 0 0.866 -0.5 0 2.5 1.5 0 -0.33333 -0.33333 0
19 'MCu1' 1 1 -0.5 -0.866 0 0.866 -0.5 0 0.5 2 0 -0.33333 -0.33333 0
20 'MCu1' 2 1 -0.5 -0.866 0 0.866 -0.5 0 0 2.5 0 -0.33333 -0.33333 0
21 'MCu1' 3 1 1 0 0 0 1 0 0.5 2.5 0 -0.33333 -0.33333 0
22 'MCu1' 1 1 -0.5 0.866 0 -0.866 -0.5 0 1.5 2 0 -0.33333 -0.33333 0
23 'MCu1' 2 1 -0.5 0.866 0 -0.866 -0.5 0 1 2.5 0 -0.33333 -0.33333 0
24 'MCu1' 3 1 -0.5 -0.866 0 0.866 -0.5 0 1.5 2.5 0 -0.33333 -0.33333 0
25 'MCu1' 1 1 1 0 0 0 1 0 2.5 2 0 -0.33333 -0.33333 0
26 'MCu1' 2 1 1 0 0 0 1 0 2 2.5 0 -0.33333 -0.33333 0
27 'MCu1' 3 1 -0.5 0.866 0 -0.866 -0.5 0 2.5 2.5 0 -0.33333 -0.33333 0
Ground state energy: -1.000 meV/spin.
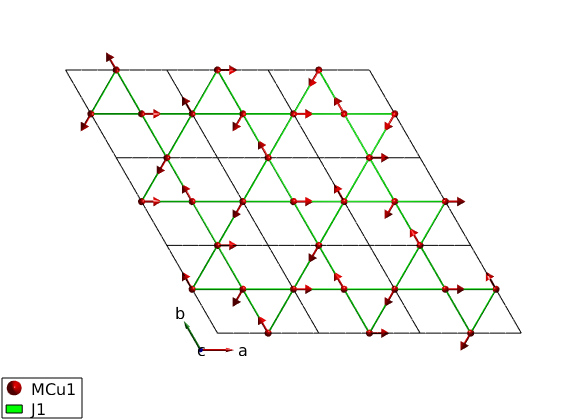
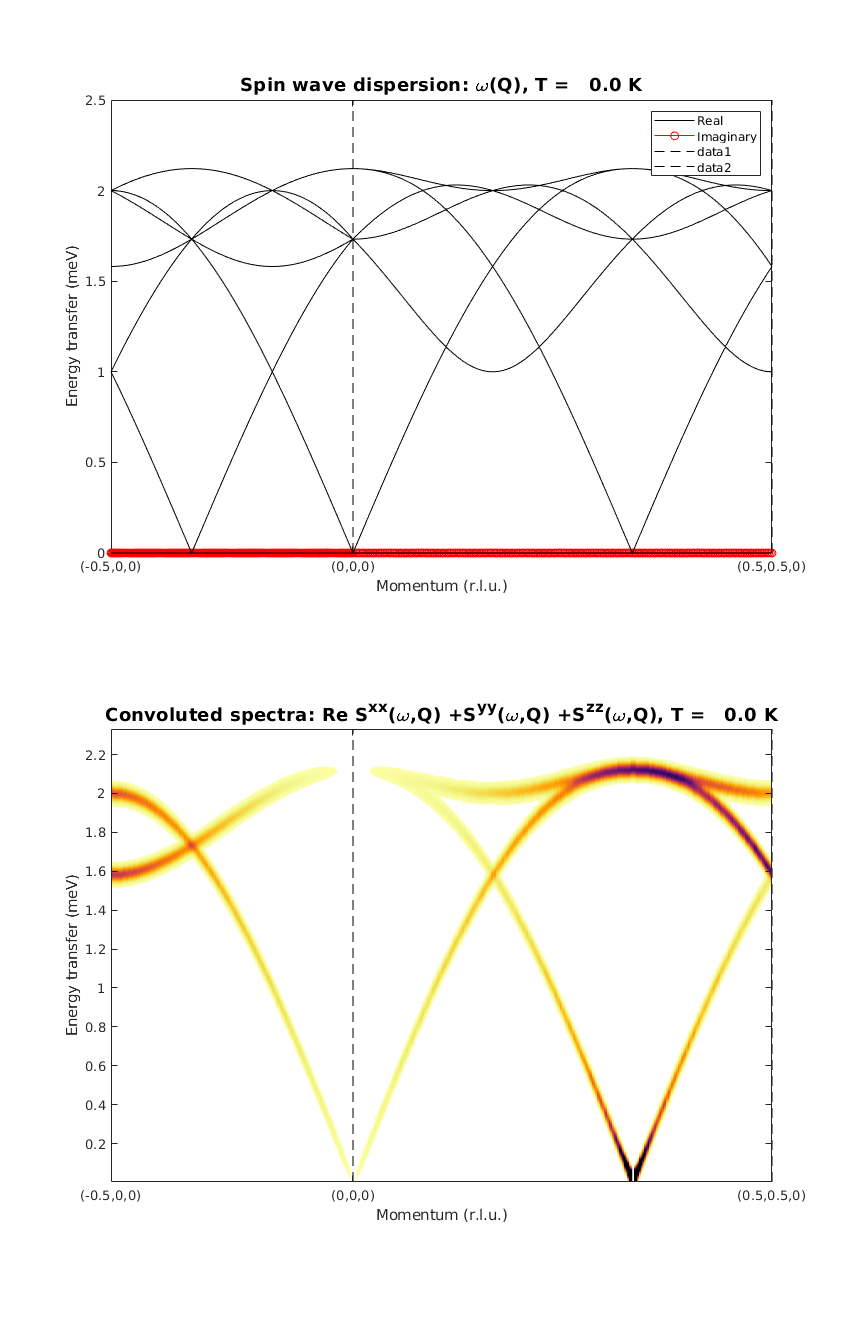
Calculate spin wave dispersion I.
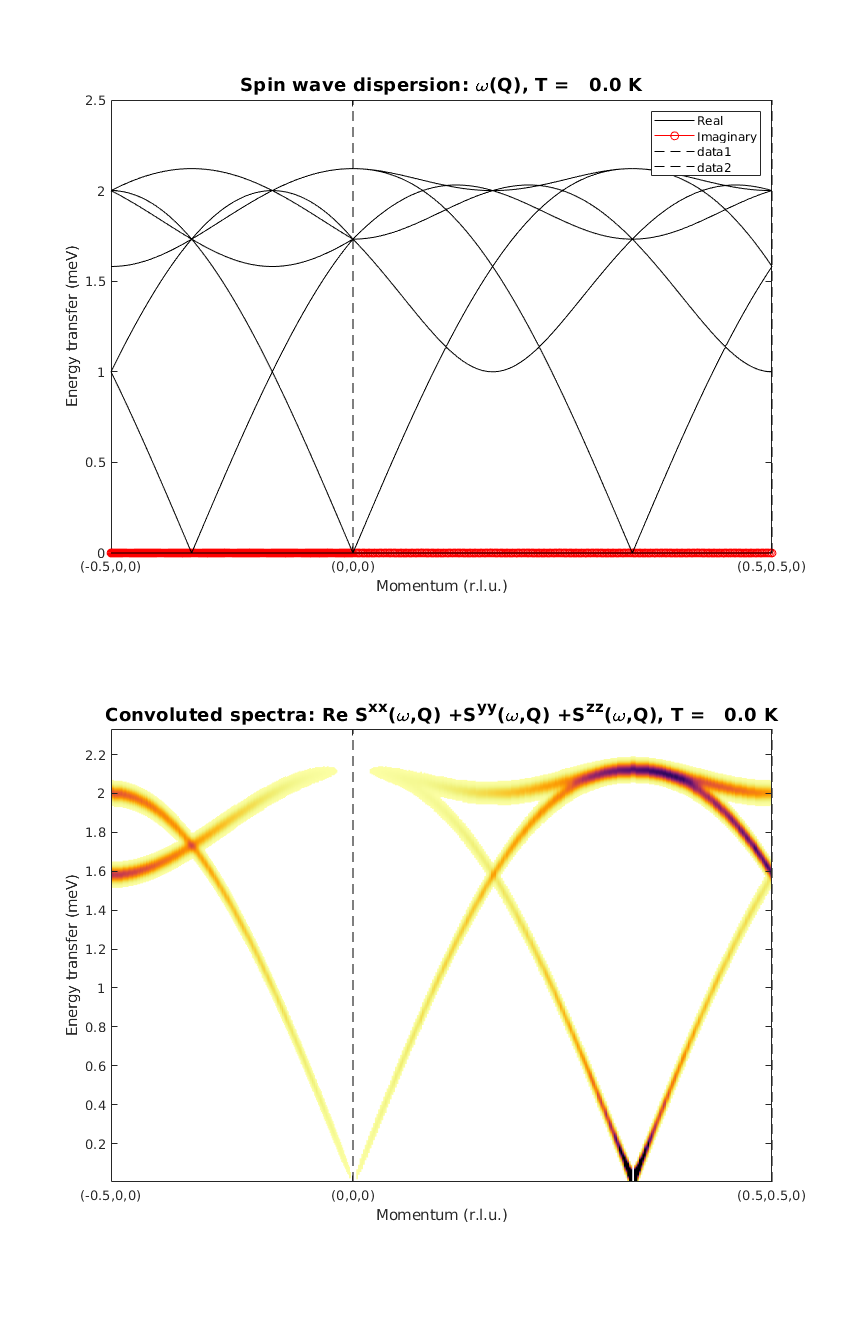
We plot the real and imaginary part of the dispersion. By observing the imaginary part of the dispersion we can ensure that we have the right magnetic ground state. After calculating the diagonal of the correlation function we can see that only a few modes have non-zero intensity.
kag33Spec = AF33kagome.spinwave({[-1/2 0 0] [0 0 0] [1/2 1/2 0] 250},'hermit',false);
kag33Spec = sw_egrid(kag33Spec,'component','Sxx+Syy+Szz','imagChk',false);
figure
subplot(2,1,1)
sw_plotspec(kag33Spec,'mode',1,'axLim',[0 2.5],'colorbar',false',...
'colormap',[0 0 0],'imag',true,'sortMode',true,'dashed',true)
subplot(2,1,2)
sw_plotspec(kag33Spec,'mode',3,'dE',0.05,'axLim',[0 2.5],'dashed',true)
swplot.subfigure(1,3,1)
colorbar off
legend off
Generate magnetic structure II.
Alternatively we can use the original unit cell, in this case the spin wave algorithm will calculate the dispersion on the assumption that the structure is incommensurate. The advantage of this method is that it produces less number of spin wave modes, more stable and faster.
S0 = [0 0 -1; 1 1 -1; 0 0 0]; AF33kagome.genmagstr('mode','helical','k',[-1/3 -1/3 0],... 'n',[0 0 1],'unit','lu','S',S0,'nExt',[1 1 1]); disp('Magnetic structure:') AF33kagome.table('mag') AF33kagome.energy plot(AF33kagome,'range',[3 3 1/2])
Magnetic structure:
ans =
3×8 table
num matom idx S realFhat imagFhat pos kvect
___ ______ ___ _ ________________________ __________________________ _________________ ________________________________
1 'MCu1' 1 1 -0.5 0.866 0 -0.866 -0.5 0 0.5 0 0 -0.33333 -0.33333 0
2 'MCu1' 2 1 -0.5 0.866 0 -0.866 -0.5 0 0 0.5 0 -0.33333 -0.33333 0
3 'MCu1' 3 1 -0.5 -0.866 0 0.866 -0.5 0 0.5 0.5 0 -0.33333 -0.33333 0
Ground state energy: -1.000 meV/spin.
Calculate spin wave dispersion II.
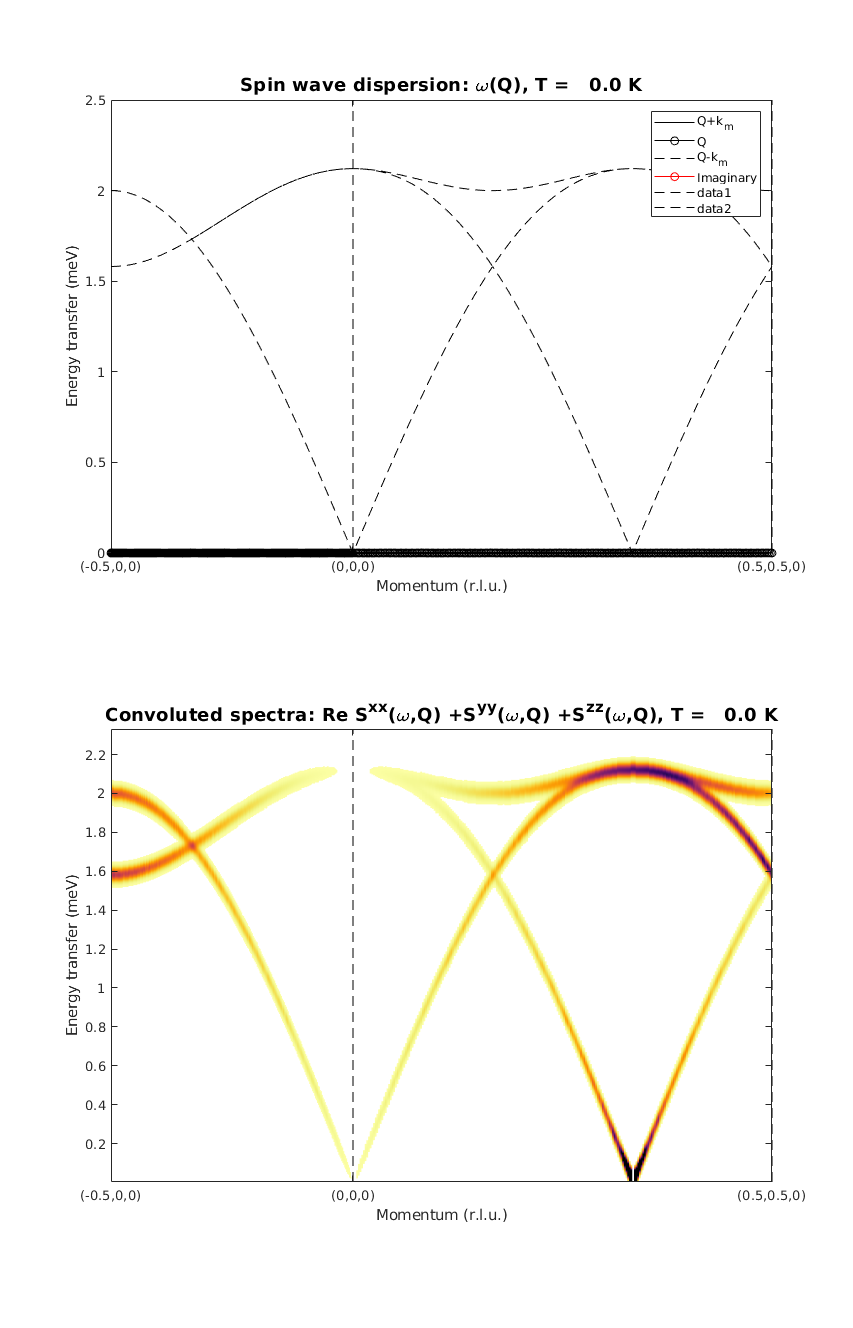
We plot the real and imaginary part of the dispersion. There are only three modes now, only the ones that have intensity. The calculated intensity map is identical to the previous calculation. Except the zero energy mode, that is missing. However this mode is not part of the inelastic spectrum. Also, this zero energy mode can be only lifted by introducing a perturbation to the spin Hamiltonia that will break the rotational symmetry of the magnetic structure. So the perturbed case can only be calculated using the magnetic supercell.
kag33Spec = AF33kagome.spinwave({[-1/2 0 0] [0 0 0] [1/2 1/2 0] 250},'hermit',false);
kag33Spec = sw_egrid(kag33Spec,'component','Sxx+Syy+Szz');
figure
subplot(2,1,1)
sw_plotspec(kag33Spec,'mode',1,'axLim',[0 2.5],'colorbar',false',...
'colormap',[0 0 0],'imag',true,'sortMode',true,'dashed',true)
subplot(2,1,2)
sw_plotspec(kag33Spec,'mode',3,'dE',0.05,'axLim',[0 2.5],'dashed',true)
colorbar off
legend off
swplot.subfigure(1,3,1)
Warning: Eigenvectors of defective eigenvalues cannot be orthogonalised at some q-point!
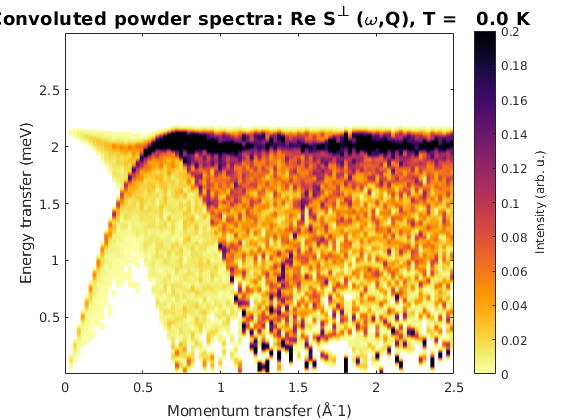
Powder spectrum
Using the small magnetic cell, the calculation of the powder spectrum is ~4.5 times faster than for the 3x3x1 magnetic supercell. The speed of the powder calculation is depending on the nomber of Q points and number of random orientations: T ~ nQ * nRand, it is mostly independent of the number size of the energy bin vector.
kag33Pow = AF33kagome.powspec(linspace(0,2.5,100),'Evect',linspace(0,3,500),... 'hermit',false,'nRand',1e2); figure sw_plotspec(kag33Pow,'axLim',[0 0.2],'dE',0.05)
Warning: Eigenvectors of defective eigenvalues cannot be orthogonalised at some q-point!
Written by Bjorn Fak & Sandor Toth 07-Jun-2014, 06-Feb-2017