Anisotropic exchange on the FM chain
Contents
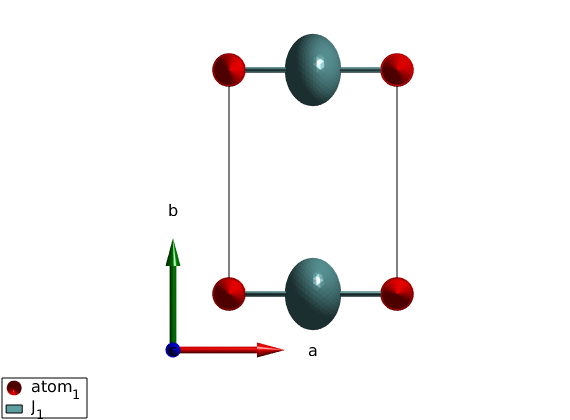
Define the lattice
fmch = spinw; fmch.genlattice('lat_const',[3 4 4]) fmch.addatom('r',[ 0 0 0],'S',1) fmch.addmatrix('label','J_1','value',diag(-[3 4 5])) fmch.gencoupling fmch.addcoupling('mat','J_1','bond',1) fmch.genmagstr('mode','helical','S',[0 0 1]') plot(fmch)
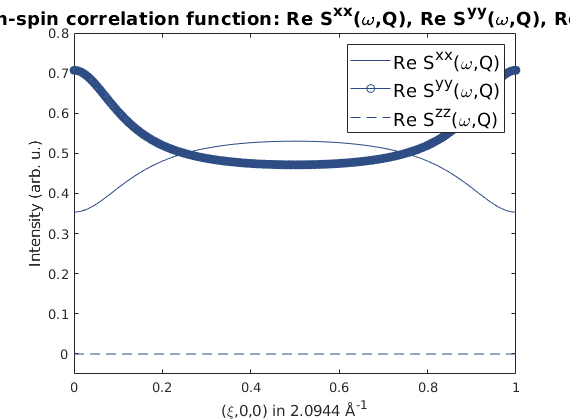
spin-spin correlation function
spec = fmch.spinwave({[0 0 0] [1 0 0] 501});
spec = sw_egrid(spec,'component',{'Sxx' 'Syy' 'Szz'});
clf
sw_plotspec(spec,'mode','int','dE',0.5);
ylim([-0.05 0.8])
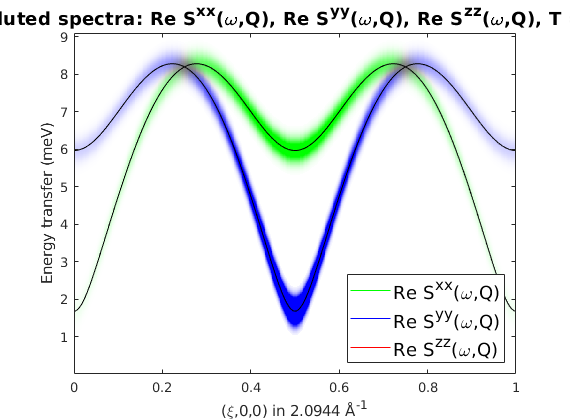
anisotropic exchange on the AFM chain
afmch = spinw; afmch.genlattice('lat_const',[3 4 4]) afmch.addatom('r',[ 0 0 0],'S',1) afmch.addmatrix('label','J_1','value',diag([3 4 4.1])) afmch.gencoupling afmch.addcoupling('mat','J_1','bond',1) afmch.genmagstr('mode','helical','S',[0 0 1]','k',[1/2 0 0],'n',[1 0 0]) %plot(afmch)
spin-spin correlation function
spec = afmch.spinwave({[0 0 0] [1 0 0] 501});
spec = sw_egrid(spec,'component',{'Sxx' 'Syy' 'Szz'});
clf
sw_plotspec(spec,'mode','disp','linestyle','-','colormap',[0 0 0])
colorbar off
legend off
sw_plotspec(spec,'mode','color','dE',0.5,'axLim',[0 1]);
hold on
hLegend = legend;
set(hLegend,'location','southeast')
Warning: The two times the magnetic ordering wavevector 2*km = G, reciproc lattice vector, use magnetic supercell to calculate spectrum!
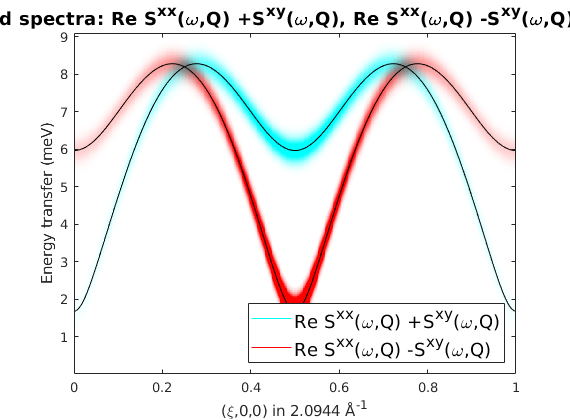
anisotropic exchange on the AFM chain
rotated anisotropy
afmch = spinw; afmch.genlattice('lat_const',[3 4 4]) afmch.addatom('r',[ 0 0 0],'S',1) R = sw_rotmatd([0 0 1],45); J1 = diag([3 4 4.1]); J1 = R*J1*R'; afmch.addmatrix('label','J_1','value',J1) afmch.gencoupling afmch.addcoupling('mat','J_1','bond',1) afmch.genmagstr('mode','helical','S',[0 0 1]','k',[1/2 0 0],'n',[1 0 0],'nEXt',[2 1 1]) %plot(afmch)
spin-spin correlation function
spec = afmch.spinwave({[0 0 0] [1 0 0] 501});
spec = sw_neutron(spec,'uv',{[1 1 0] [-1 1 0]},'pol',true);
spec = sw_egrid(spec,'component',{'Sxx+Sxy' 'Sxx-Sxy'});
clf
sw_plotspec(spec,'mode','disp','linestyle','-','colormap',[0 0 0])
colorbar off
legend off
sw_plotspec(spec,'mode','color','dE',0.5,'axLim',[0 1]);
hold on
hLegend = legend;
set(hLegend,'location','southeast')