Requirements and Installation
What you need
SpinW can be used in two different ways:
- The best is to run it from a recent version of Matlab (newer than R2014a), however this requires a valid license.
- The alternative way is to run pySpinW from Python which does not require Matlab license and it can also be used for distributed computing.
The symbolic calculation mode also needs the Symbolic Math Toolbox installed.
Installation
The latest version of SpinW can be downloaded from [https://github.com/tsdev/spinw/releases](https://github.com/tsdev/spinw/releases. Steps to install:
- extract the
.zipfile into any local folder - add the folder to the Matlab search path using
addpath(genpath(MYSPINWFOLDER)) - recommended to copy the above command into the
startup.mfile
Updating
Since SpinW is under active development, there are regular updates (new features, bug fixes). To update your local copy of SpinW do the following:
- execute the sw_update function in the Matlab Command Window, this will check for the latest available version and downloads it into a new subfolder beside the current SpinW installation (sw_rootdir returns the current path) and adds the new files to the Matlab search path
- to make the new path permanent, edit your
startup.mfile as written above - execute the
clear classescommand in the Command Window to clear the Matlab cache of user defined classes
Hello World!
It is possible to create, solve and plot a spin wave model in a single line of code using SpinW! For example the following line will solve the spin wave dispersion of the triangular lattice antiferromagnet (TLA) along the direction in reciprocal space:
sw_plotspec(spinwave(sw_model('triAF',1),{[0 0 0] [1 1 0]}))
![sw_plotspec(spinwave(sw_model('triAF',1),{[0 0 0] [1 1 0]}))](images/generated/introdu_1.png)
This line includes 3 functions:
- sw_model generates one of the predefined spin Hamiltonians, in this case a TLA with meV first neighbor antiferromagnetic exchange
- spinw.spinwave calculates the spin wave dispersion between the and reciprocal space points
- sw_plotspec plots the spin wave dispersion
The following documentation will show how to prepare more complicated spin Hamiltonians.
Get help
The fastest way to get help is to access this documentation via the swdoc command. To jump directly to the help of a specific function use:
swdoc funName
Alternatively the swhelp command will show the help text in the MATLAB Command Window that works the same way as the MATLAB built-in [matlab:help] command:
swhelp funName
If you didn’t find the answer, you can ask questions on the SpinW Forum as well.
If you find a bug, please submit a bug report on GitHub, this is the fastest route to have it fixed.
Handle Class
The central part of SpinW is the spinw object which stores the spin Hamiltonian and defines operations on it. It is important to know that unlike most Matlab variable, the spinw object is handle class type. This means that a simple copy command:
swobj2 = swobj1
just creates a copy of the handle, but still swobj1 and swobj2 will point to the same location in memory. To disentangle the two variables, the spinw.copy method will do:
swobj3 = swobj1.copy
now swobj3 is an independent copy of swobj1.
The main advantages of handle class:
- object methods can be called as
obj.method(parameter)for non-handle classes the returned object has to be saved:
obj = method(obj,parameter) - working with handle classes saves memory, as we create a copy of the object less often
Matrix dimensions
Since Matlab is optimized for working with arrays efficiently, many of input and output arguments of the spinw methods take multidimensional arrays. Thus it is important to introduce some definitions. Throughout the documentation the word matrix will refer to multidimensional arrays where the dimensions are denoted in square brackets, e.g. means a matrix with 3 rows and variable number of columns, this is a 2D matrix but there are matrices with higher dimensions, e.g. the spin-spin correlation function can be represented by a matrix with dimensions of , which corresponds to , where and is indexed by the mode number of is indexed on a predefined grid. Since the sequence of dimensions is not fixed by math, a representation of the spin-spin correlation function with a matrix with dimensions of is equally valid. To minimize the guessing, each matrix is SpinW is defined such that the variable size dimensions are the rightmost. For example a list of position vectors will be stored in a matrix with dimensions of , a list of matrices will be stored in a matrix with dimensions of .
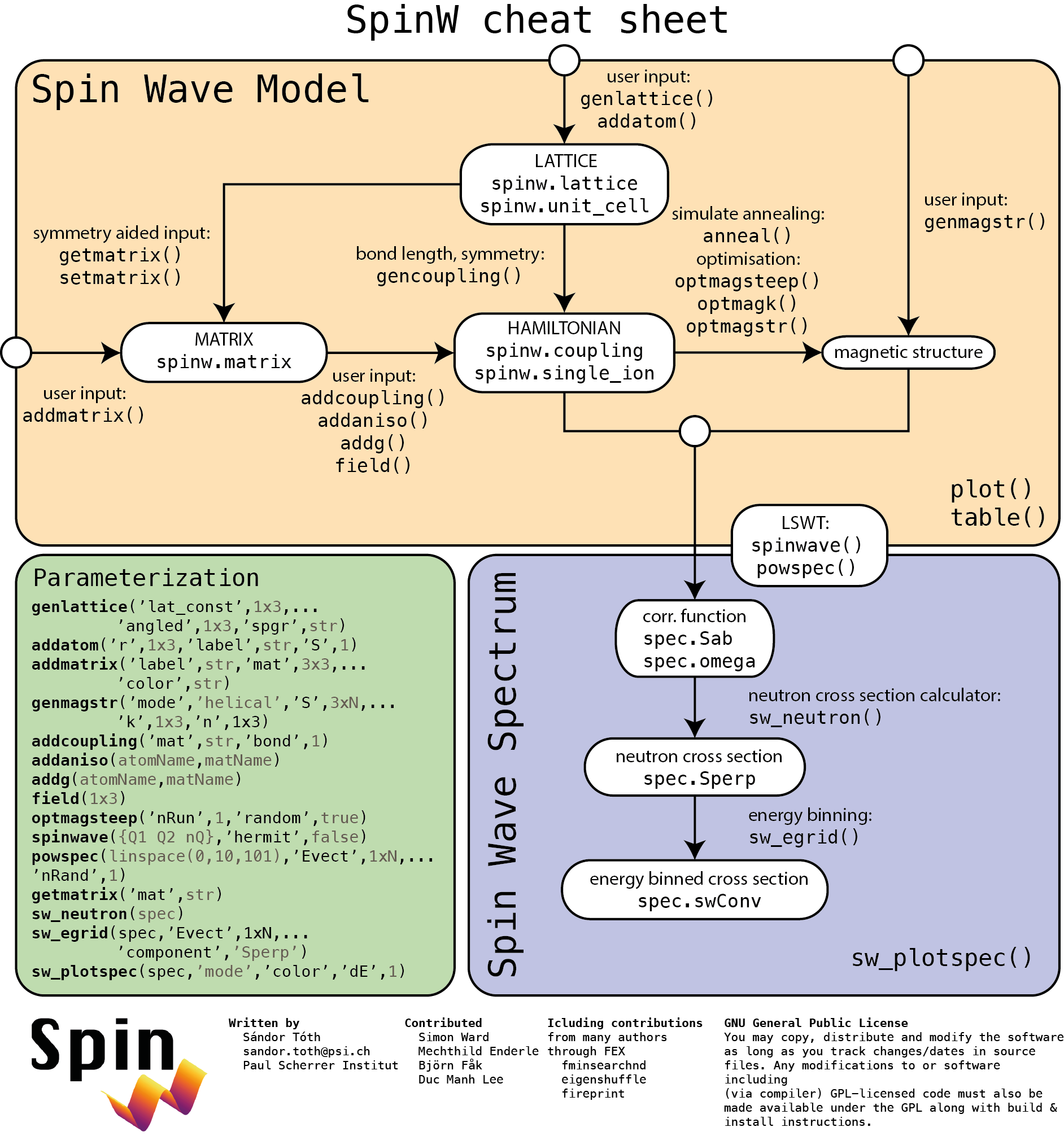
SpinW Cheat Sheet
The SpinW cheat sheet shows the most common commands and their list of input parameters with the required input matrix dimensions. Print it and keep it close to your desk!